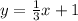To determine the equation of the line that has slope m=1/3 and passes through the point (3,2) you have to use the point-slope form:

Where
m is the slope of the line
(x₁,y₁) are the coordinates of one point of the line
Replace the formula above with the known information about the line:
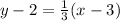
Next is to write the equation in slope-intercept form, which means that you have to leave the y term alone on the left side of the equation and all other terms have to be on the right side.
-First, distribute the multiplication on the parentheses term:
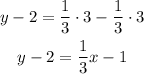
-Second, pass "-2" to the right side of the equation by applying the opposite operation, "+2", to both sides of the equal sign:
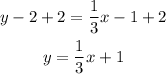
So, the equation of the line with slope 1/3 that passes through the point (3,2), expressed in slope-intercept form is: