Question

ANSWER QUESTION 3 PHOTO ATTACHEDFAST REPLY = BETTER RATINGTHANK YOU!

Answer 1

Given

`f(x)=xe^(7x)`

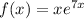
Calculate the second derivative of f(x), as shown below

`\begin{gathered} \Rightarrow f^(\prime)(x)=e^(7x)+7xe^(7x) \\ and \\ \Rightarrow f^(\prime)^(\prime)(x)=7e^(7x)+7(e^(7x)+7xe^(7x)) \\ \Rightarrow f^(\prime)^(\prime)(x)=14e^(7x)+49xe^(7x) \end{gathered}`

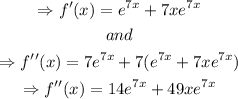
Then, find the interval such that f''(x)>0 in order to find where f(x) is concave up,

`\begin{gathered} 14e^(7x)+49xe^(7x)>0 \\ \Rightarrow2e^(7x)+7x*e^(7x)>0 \\ and \\ e{}^(7x)>0,x\in\Re \end{gathered}`

Then,

`\begin{gathered} 2e^(7x)>-7xe^(7x) \\ \Rightarrow2>-7x \\ \Rightarrow x>-(2)/(7) \end{gathered}`

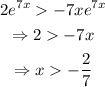
Therefore, f(x) is concave up when x in (-2/7, +infinite).

In the case of concavity down,

`\begin{gathered} f^(\prime)^(\prime)(x)<0 \\ \Rightarrow2e^(7x)+7x*e^(7x)<0 \\ \Rightarrow2+7x<0 \\ \Rightarrow-(2)/(7)>x \end{gathered}`

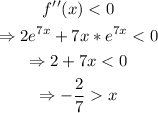
Thus, f(x) is concave down when x in (-infinite, -2/7).

The answer is the fifth and last option (top to bottom).