Question

A person with a mass of 78.0 kg is standing on a bathroom scale in an elevator that is accelerating downwards at a rate of 1.25 m/s2What is the normal force? (the reading on the scale)(input your answer with one decimal place)

Answer 1

Given:

• Mass, m = 78.0 kg

,

• Acceleration = 1.25 m/s²

Let's find the normal force.

To find the normal force, apply the formula for Newton's second law:

`\begin{gathered} \Sigma F_y=ma_y \\ \\ F-mg=-ma \end{gathered}`

Where:

m is the mass of the person = 78.0 kg

a is the acceleration = 1.25 m/s²

g is acceleration due to gravity = 9.8 m/s²

F is the normal force

Thus, we have:

`\begin{gathered} F=mg-ma \\ \\ F=m(g-a) \\ \\ F=78(9.8-1.25) \end{gathered}`

Solving further:

`\begin{gathered} F=78(8.55) \\ \\ F=666.9\text{ N} \end{gathered}`

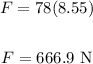
The reading on the scale will be in kilograms.

Hence, we have:

`m=(N)/(g)=(666.9)/(9.8)=68.1\text{ kg}`

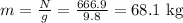
Therefore, the reading on the scale will be 68.1 kg or 666.9 N

ANSWER:

666.9 N