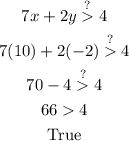Question

X-6y>57x+2y>4Is (10,-2) a solution of the system?

Answer 1

To check if (10, -2) is a solution to the system, we have to replace x with "10" and y with "-2" and see if the inequalities hold true.

If both the inequalities hold true, then definitely (10, -2) is a solution!

Let's check the first inequality:

`\begin{gathered} x-6y\stackrel{?}{>}5 \\ 10-6(-2)\stackrel{?}{>}5 \\ 10+12\stackrel{?}{>}5 \\ 22>5 \\ \text{True} \end{gathered}`

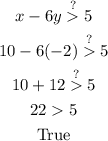
Now, let's check the second inequality:

`\begin{gathered} 7x+2y\stackrel{?}{>}4 \\ 7(10)+2(-2)\stackrel{?}{>}4 \\ 70-4\stackrel{?}{>}4 \\ 66>4 \\ \text{True} \end{gathered}`