Our first approach will be to get the slant height, i.e. the sides of the triangle. We can get this via the sine rule as:
We can get the side of the isosceles to be:
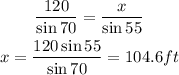
Now we need to find the perpendicular height.
To do that, we need to find the length of the diagonal of the base. We will apply the Pythagoras theorem.
This is given as:
![\begin{gathered} d=\sqrt[]{o^2+a^2} \\ \text{ Where:} \\ o=\text{opposite = length of base} \\ a=\text{adjacent = length of base} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5e6akso3zn791b4it2dr79kqnd7xigdm4e.png)
![\begin{gathered} d=\sqrt[]{120^2+120^2} \\ d=170\text{ ft} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y7z5tbhmhqseslzrag2oys5tqb2hsdio6i.png)
Next, we plot the triangle that will help us get our perpendicular height.
We now find h.
![\begin{gathered} h=\sqrt[]{104.6^2-85^2} \\ h=60.96\text{ ft} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/nlhx66c1admvnxgsnulm9i5gl52gmgwngo.png)
The perpendicular height is 60.96 ft