Answer:
20
Explanation:
Let:
• NP = The non-park goers.
,
• NB = The non-beach goers.
,
• NC = The non-cottage goers.
The Venn diagram below is used to represent the given information:
Given:
• There are 10 non-park goers: a+b+c+g=10
,
• There are 9 non-beach goers: b+d+e+g=9
,
• There are 11 non-cottages goers: c+e+f+g=11
,
• There are 3 non-park and non-beach goers: b+g=3
,
• There are 4 non-beach and non-cottage goers: e+g = 4
,
• There are 6 non-park and non-cottage goers: c+g=6
,
• There is 1 non-park, non-beach, and non-cottage goer: g=1
,
• There are 2 who are neither a non-park, non-beach, or non-cottage goer: h=2
So, the total number of family members will be:
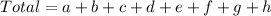
Since g=1:
![\begin{gathered} b+g=3\implies b+1=3\implies b=2 \\ c+g=6\operatorname{\implies}c+1=6\operatorname{\implies}c=5 \\ e+g=4\operatorname{\implies}e+1=4\operatorname{\implies}e=3 \end{gathered}]()
Next:
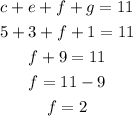
Next:
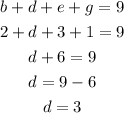
Therefore:
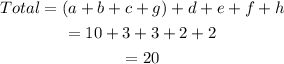
The total number of family members is 20.