Question

X= 7 4. Find the equation of a line passing through (5, -6) perpendicular (b) 3x + 5y = (d) 7x - 12y (f) x = 7 (a) 2x + y = 12 (c) x + 3y = 8 (e) 2y = 5 Find the equation of the line connecting the points of intersect (a) S x + y = 4 S 3x - y = 12 (b) Sy= and 2x=6 = -6 X=

Answer 1

Given data:

The first set of equations are x+y=4, and x=6.

The second set of equations are 3x-y=12 and y=-6.

The point of intersection of first set of te equations is,

6+y=4

y=-2

The first point is (6, -2).

The point of intersection of second set of te equations is,

3x-(-6)=12

3x+6=12

3x=6

x=2

The second point is (2, -6).

The equation of the line passing through (6, -2) and (2, -6) is,

`\begin{gathered} y-(-2)=(-6-(-2))/(2-6)(x-6) \\ y+2=(-6+2)/(-4)(x-6) \\ y+2=x-6 \\ y=x-8 \end{gathered}`

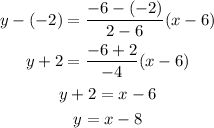
Thus, the required equation of the line is y=x-8.