Question

Write a quadratic equation that has two imaginary solutions

Answer 1

We are asked to determine a quadratic equation that has two imaginary solutions. Let's suppose that the solution of the equation is the following:

`x=\pm i`

This means that the two imaginary solutions are "i" and "-i". Now, we use the following:

`\pm i=\sqrt[]{-1}`

Substituting we get:

`x=\sqrt[]{-1}`

Squaring both sides:

`x^2=-1`

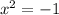
Now, we add 1 to both sides:

`x^2+1=0`

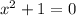
And thus we have obtained a quadratic equation with two imaginary solutions.