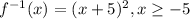Question

I’m struggling with my homework assignment, can anyone help me?

Answer 1

We can find the inverse function writing f(x) as y in the original function and then changing x with y and isolating y again, so

`y=\sqrt[]{x}-5`

Changing y with x we have

`x=\sqrt[]{y}-5`

Now we must get y on one side of the equation again, then

`\begin{gathered} x=\sqrt[]{y}-5 \\ x+5=\sqrt[]{y} \\ (\sqrt[]{y})^2=(x+5)^2 \\ y=(x+5)^2 \end{gathered}`

The domain of the inverse function in the image of the original function f, the image of f is x ≥ -5, then the domain of the inverse of will be x ≥ -5, so our answer is

`f^(-1)(x)=(x+5)^2,x\ge-5`