Question

Use inverse matrix to solve the linear system. Solve #19

Answer 1

19)

The given system of equations is,

`\begin{gathered} 4x-3y=11 \\ 5x-2y=12 \end{gathered}`

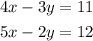
The above system of equations can be written in matrix form as,

`\begin{bmatrix}{4} & {-3} & {} \\ {5} & {-2} & {} \\ {} & {} & \end{bmatrix}\begin{bmatrix}{x} & {} & {} \\ {y} & & {} \\ {} & {} & \end{bmatrix}=\begin{bmatrix}{11} & {} & \\ {12} & {} & \\ {} & {} & \end{bmatrix}\text{ -----(1)}`

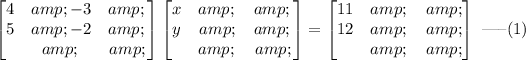
Here,

`A=\begin{bmatrix}{4} & {-3} & {} \\ {5} & {-2} & {} \\ {} & {} & \end{bmatrix},\text{ X=}\begin{bmatrix}{x} & {} & {} \\ {y} & & {} \\ {} & {} & \end{bmatrix}\text{ },\text{ B=}\begin{bmatrix}{11} & {} & \\ {12} & {} & \\ {} & {} & \end{bmatrix}`

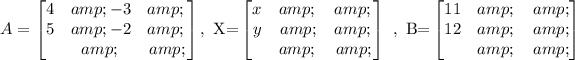
Therefore, equation (1) can be written as,

`AX=B`

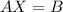
Therefore,

`X=A^(-1)B\text{ -------(2)}`

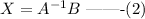
Now, we need to calculate the inverse of A.

(Note:

Let a 2x2 matrix P is of the form given below.

`P=\begin{bmatrix}{a} & {b} & {} \\ {c} & {d} & {} \\ {} & {} & {}\end{bmatrix}`

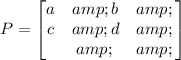
The inverse of the matrix P is,

`\begin{gathered} P^(-1)=(1)/(|P|)\begin{bmatrix}{d} & {-b} & {} \\ {-c} & {a} & {} \\ {} & {} & {}\end{bmatrix} \\ =(1)/(ad-bc)\begin{bmatrix}{d} & {-b} & {} \\ {-c} & {a} & {} \\ {} & {} & {}\end{bmatrix} \end{gathered}`

)

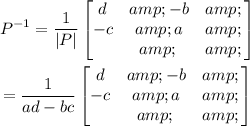
Similar to the inverse matrix of 2x2 matrix P, the inverse matrix of A can be written as,

`\begin{gathered} A^(-1)=(1)/(4*(-2)-(-3)*5)\begin{bmatrix}{-2} & {3} & {} \\ {-5} & {4} & {} \\ {} & {} & {}\end{bmatrix} \\ =(1)/(-8+15)\begin{bmatrix}{-2} & {3} & {} \\ {-5} & {4} & {} \\ {} & {} & {}\end{bmatrix} \\ =(1)/(7)\begin{bmatrix}{-2} & {3} & {} \\ {-5} & {4} & {} \\ {} & {} & {}\end{bmatrix} \\ =\begin{bmatrix}{(-2)/(7)} & {(3)/(7)} & {} \\ {(-5)/(7)} & {(4)/(7)} & {} \\ {} & {} & {}\end{bmatrix} \end{gathered}`

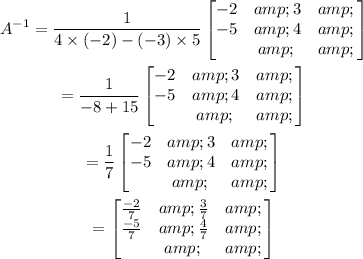
Now, put the values in equation (2) to find the solution to the system of equations.

`\begin{gathered} X=A^{-1^{}}B \\ \begin{bmatrix}{x} & {} & {} \\ {y} & & {} \\ {} & {} & \end{bmatrix}=\begin{bmatrix}{(-2)/(7)} & {(3)/(7)} & {} \\ {(-5)/(7)} & {(4)/(7)} & {} \\ {} & {} & {}\end{bmatrix}\begin{bmatrix}{11} & {} & \\ {12} & {} & \\ {} & {} & \end{bmatrix} \\ =\begin{bmatrix}{(-2)/(7)*11+(3)/(7)*12} & {} & {} \\ {(-5)/(7)*11+(4)/(7)*12} & & {} \\ {} & {} & {}\end{bmatrix} \\ =\begin{bmatrix}{(-22)/(7)+(36)/(7)} & {} & {} \\ {(-55)/(7)+(48)/(7)} & & {} \\ {} & {} & {}\end{bmatrix} \\ =\begin{bmatrix}{(-22+36)/(7)} & {} & {} \\ {(-55+48)/(7)} & & {} \\ {} & {} & {}\end{bmatrix} \\ =\begin{bmatrix}{(14)/(7)} & {} & {} \\ {(-7)/(7)} & & {} \\ {} & {} & {}\end{bmatrix} \\ \begin{bmatrix}{x} & {} & {} \\ {y} & & {} \\ {} & {} & \end{bmatrix}=\begin{bmatrix}{2} & {} & {} \\ {-1} & & {} \\ {} & {} & {}\end{bmatrix} \end{gathered}`

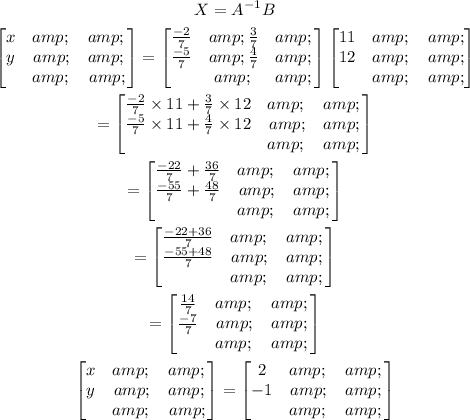
Therefore, the solution to the system of equations using inverse matrix is x=2 and y=-1.