Question

Randall is buying house for $242,000. His down payment is 55% of the price. The mortgage ratefor a 5-year term is 8.2% per annum, compounded semi-annually, amortized over 25 years, andpaid monthly.a) For how much is the mortgage, once the down payment is deducted and compounded?b) How much are the monthly payments,,,,,

Answer 1

Given the question in the image, the following are the solution steps to answer the question.

STEP 1: Write the given values

`\begin{gathered} Total\text{ payment}=242000 \\ down\text{ payment}=55\% \\ rate\text{ for compunding}=8.2\%=(8.2)/(100)=0.082 \\ n=2\text{ since it is compounded semi-annually} \\ t=5\text{ years} \end{gathered}`

STEP 2: Find the mortgage value

`mortgage\text{ }value=Total\text{ payment}-Down\text{ payment}`

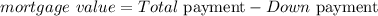
Down payment will be calculated:

`\begin{gathered} 55\%\text{ of \$242000} \\ (55)/(100)\cdot242000=0.55\cdot242000=\text{ \$}133100 \end{gathered}`

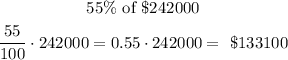
To calculate the mortgage value, we first calculate the compounded amount,

`\begin{gathered} A = P(1 + (r)/(n))^(nt) \\ A=108900\cdot(1+(0.082)/(2))^(2\cdot5) \\ A=108900\cdot(1.041)^(10) \\ A=162755.3131\approx\text{ \$}162755.31 \end{gathered}`

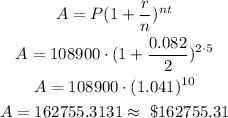
Hence, the mortgage value will be approximately $162755.31

Then we calculate the monthly payments

Number of months between 25 years will be:

`\begin{gathered} 1\text{ year}=12\text{ months} \\ 25\text{ years}=25\cdot12=300\text{ months} \end{gathered}`

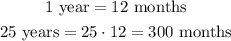
Therefore, the monthly payments will be:

`\text{ }\frac{\text{ \$}162755.31}{300}=542.5177\approx\text{ \$}542.52`

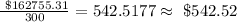
The monthly payments will be approximately $542.52