If at day 1 we get 1% better than in the day 0, we will be:
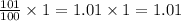
1.01 better on day 1 than on day 0.
If we get 1% better on day 2 than on day 1, then by day 2 we would be:
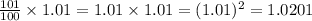
1.0201 times better on day 2 than on day 0.
After n days, we would have to multiply 1 by 1.01 n times, so by day n we would be:
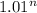
times better than on day 0.
Calculate 1.01^365 to find how many times better we would be one year after day 0:
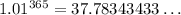
Therefore, we would get 37.78 times better by day 365, which is after one year.