Question

Find the half-life (in hours) of a radioactive substance that is reduced by 5 percent in 75 hours.half life = ___ include units

Answer 1

Let's list down the given information.

Time = 75 hours

Final Value = reduced by 5% = 95%

To get the half life, the formula is:

`t=(\ln 0.5)/(k)`

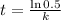
Before we can get the half-life, we need to get the value of k or the decay rate first. The formula is:

`k=(\ln A)/(t)`

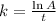
where A is the final value in percentage and t = time. Since we have this information above, let's plug it in the formula and solve for k.

`k=(\ln0.95)/(75)=-0.0006839105918`

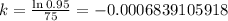
Now that we have the value of "k", let's solve for "t" using the formula stated above as well.

`t=(\ln 0.5)/(k)=(\ln 0.5)/(-0.0006839105918)=1013.51`

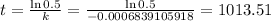
Hence, the half life of the radioactive substance is approximately 1,013.51 hours or 1,013 hours and 30 minutes.