Question

Fill in the following values for a 45-45-90 triangle Leg Leg Hypotenuse 5 А B C С D 32 Fill in the following values for a 30-60-90 triangle Short Leg Long Leg Hypotenuse 6 E H 20 G

Answer 1

First Part 45-45-90 Triangle

first triangle

where the two angles different to 90° are same, the measure of the legsof the triangle are the same

then

`A=5`

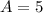
and to calculate B or the hypotenuse we use pythagoras

`a^2+b^2=h^2`

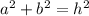
where a and b are legs and h the hypotenuse

replacing

`\begin{gathered} 5^2+5^2=h^2 \\ 25+25=h^2 \\ 50=h^2 \\ h=\sqrt[]{50} \\ h=5\sqrt[]{2} \end{gathered}`

the hypotenuse or B is

`B=5\sqrt[]{2}`

Second triangle

legs of the triangle have the same value then if we apply pythagoras

`a^2+b^2=h^2`

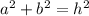
and replace the legs with the same value(a)

`\begin{gathered} a^2+a^2=h^2 \\ 2a^2=h^2 \end{gathered}`

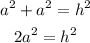
we can replace the hypotenuse and solve a

`\begin{gathered} 2a^2=(3\sqrt[]{2})^2 \\ 2a^2=18 \\ a^2=(18)/(2) \\ \\ a=\sqrt[]{9} \\ a=3 \end{gathered}`

value of each leg is 3 units, then

`C=D=3`

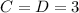
Second part 30-60-90 triangle

First triangle

we use trigonometric ratios to solve, for example I can use tangent for the angle 60 to find E

`\tan (\alpha)=(O)/(A)`

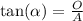
where alpha is the angle, O the oppiste side of the angle and A the adjacet side of the angle

using angle 60°

`\begin{gathered} \tan (60)=(E)/(6) \\ \\ E=6\tan (60) \\ \\ E=6\sqrt[]{3} \end{gathered}`

now using sine we calculate F or the hypotenuse

`\sin (\alpha)=(O)/(H)`

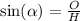
where alpha is the angle, O the opposite side from the angle and H the hypotenuse

using angle 60°

`\begin{gathered} \sin (60)=(E)/(F) \\ \\ F=(E)/(\sin (60)) \\ \\ F=\frac{6\sqrt[]{3}}{\sin (60)} \\ \\ F=12 \end{gathered}`

Second triangle

we use sine with 60° to find H

`\begin{gathered} \sin (\alpha)=(O)/(h) \\ \\ \sin (60)=(H)/(20) \\ \\ H=20\sin (60) \\ H=10\sqrt[]{3} \end{gathered}`

use cosine with 60° to find G

`\begin{gathered} \cos (\alpha)=(A)/(h) \\ \\ \cos (60)=(G)/(20) \\ \\ G=20\cos (60) \\ \\ G=10 \end{gathered}`

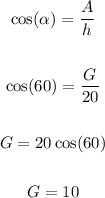
Final Values

`\begin{gathered} A=5 \\ B=5\sqrt[]{2} \\ C=3 \\ D=3 \\ E=6\sqrt[]{3} \\ F=12 \\ G=10 \\ H=10\sqrt[]{3} \end{gathered}`