Question

Given ST is tangent to circle Q, find the value of r

Answer 1

Given the figure of the circle Q

As shown, ST is tangent to circle Q

So, ST is perpendicular to the radius QS

So, the triangle QST is a right-angle triangle

We can apply the Pythagorean theorem where the legs are QS and ST

And the hypotenuse is QT

The side lengths of the triangle are as follows:

QS = r

ST = 48

QT = r + 36

So, we can write the following equation:

`\begin{gathered} QT^2=QS^2+ST^2 \\ (r+36)^2=r^2+48^2 \end{gathered}`

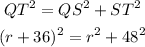
Expand then simplify the last expression:

`\begin{gathered} r^2+2*36r+36^2=r^2+48^2 \\ r^2+72r+1296=r^2+2304 \end{gathered}`

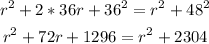
Combine the like terms then solve for (r):

`\begin{gathered} r^2+72r-r^2=2304-1296 \\ 72r=1008 \\ \\ r=(1008)/(72)=14 \end{gathered}`

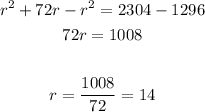
So, the answer will be r = 14