We were given:
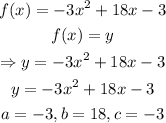
We will calculate the minimum point as shown below:

This quadratic equation opens downward because the value of ''a'' is negative. Hence, the function only has a maximum point, it does not have a minimum point
The maximum value of the function is 24 and it occurs at x equals 3