Question

Find the zeros of the function. You may want to view the graph of the function to help you identifythe real root, then use it to depress the polynomial & find the remaining roots.I

Answer 1

We must find the zeros of the following function:

`f(x)=x^3-x^2-11x+15.`

1) First, we plot a graph of the function:

From the graph, we see that the function crosses the x-axis at x = 3, so x = 3 is one of the zeros of the function.

2) Because x = 3 is a zero of the function, we can factorize the function in the following way:

`f(x)=x^3-x^2-11x+15=(x^2+b\cdot x+c)\cdot(x-3)\text{.}`

To find the coefficients b and c, we compute the product of the parenthesis and then we compare the different terms:

`f(x)=x^3-x^2-11x+15=x^3+(b-3)\cdot x^2+(c-3b)\cdot x-3c.`

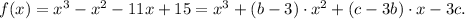
To have the same expressions at both sides of the equality we must have:

`\begin{gathered} -3c=15\Rightarrow c=-(15)/(3)=-5, \\ b-3=-1\Rightarrow b=3-1=2. \end{gathered}`

So we have the following factorization for the function f(x):

`f(x)=(x^2+2x-5)\cdot(x-3)\text{.}`

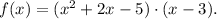
3) To find the remaining zeros, we compute the zeros of:

`(x^2+2x-5)\text{.}`

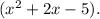
The zeros of this 2nd order polynomial are given by:

`x=\frac{-b\pm\sqrt[]{b^2-4\cdot a\cdot c}}{2a},`

where a, b and c are the coefficients of the polynomial. In this case we have a = 1, b = 2 and c = -5. Replacing these values in the formula above, we get:

s