Simplify the expression `2\sqrt{a^{2}b^{8}}\left(ab^{3}\right)^{-1}`You may type many lines to show your work. Enter equations inside the text using the square-root button below…

Question

asked Sep 12, 2023 150k views

1 Answer

← Prev Question Next Question →

Ask a Question

Gruenewa · Answer 1 · 2023-09-19T05:20:58+0000

ANSWER

2b

Step-by-step explanation

To simplify this expression, we have to apply some of the exponents' properties. First, the square root is a fractional exponent,

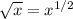
So we can rewrite the expression as,

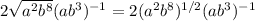
2√(a^2b^8)(ab^3)^(-1)=2(a^2b^8)^(1/2)(ab^3)^(-1)

Then, we can distribute the exponents into the multiplication,

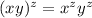
In this problem,

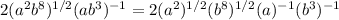
2(a^2b^8)^(1/2)(ab^3)^(-1)=2(a^2)^(1/2)(b^8)^(1/2)(a)^(-1)(b^3)^(-1)

Exponents of exponents are multiplied,

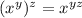
In this problem,

$2(a^2)^(1/2)(b^8)^(1/2)(a)^(-1)(b^3)^(-1)=2\cdot a^(2\cdot1/2)\operatorname{\cdot}b^{8\operatorname{\cdot}1/2}\operatorname{\cdot}a^(-1)\operatorname{\cdot}b^{3\operatorname{\cdot}(-1)}$

Simplify if possible,

$2\cdot a^(2\cdot1/2)\operatorname{\cdot}b^{8\operatorname{\cdot}1/2}\operatorname{\cdot}a^(-1)\operatorname{\cdot}b^{3\operatorname{\cdot}(-1)}=2\cdot a^1\operatorname{\cdot}b^4\operatorname{\cdot}a^(-1)\operatorname{\cdot}b^(-3)$

Now, the product of two powers with the same base is equal to the base raised to the sum of the exponents,

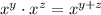
$x^y\cdot x^z=x^(y+z)$

In this problem,

$2\cdot a^1\operatorname{\cdot}b^4\operatorname{\cdot}a^(-1)\operatorname{\cdot}b^(-3)=2\cdot a^(1-1)\operatorname{\cdot}b^(4-3)$

Solve the subtractions,

$2\cdot a^(1-1)\operatorname{\cdot}b^(4-3)=2\cdot a^0\cdot b^1=2b$

Hence, the simplified expression is 2b.

Simplify the expression `2\sqrt{a^{2}b^{8}}\left(ab^{3}\right)^{-1}`You may type many lines to show your work. Enter equations inside the text using the square-root button below…

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

Please log in or register to add a comment.

No related questions found

Categories

Other Questions