The Solution:
Given the equation below:
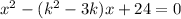
We are required to find the value of k that will make the sum of the solutions to be 10.
Step 1:
Let:
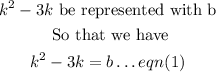
So, the given equation becomes:
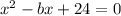
We shall the Quadratic Formula Method to solve for x in terms of b.
In this case,
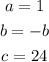
Substituting, we get
![x=\frac{-b\pm\text{ }\sqrt[]{(-b)^2-(4*1*24)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/xvgzkq0eykxy8dvovzztzi1h2ld1h42o5y.png)
![x=\frac{-b\pm\text{ }\sqrt[]{b^2-96}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/4a73u78mknx8tlwf60gexz2fwkiqdmje24.png)
So, the solutions to the given equation are:
![\begin{gathered} x=\frac{-b+\text{ }\sqrt[]{b^2-96}}{2} \\ \text{ or} \\ x=\frac{-b-\text{ }\sqrt[]{b^2-96}}{2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5y9qjtzw8jtm3klhfctfr3w6kqf02xqdzi.png)
Equating their sum to 10.
![\begin{gathered} \frac{-b+\text{ }\sqrt[]{b^2-96}}{2}+\frac{-b-\text{ }\sqrt[]{b^2-96}}{2}=10 \\ \\ \\ \frac{-b+\text{ }\sqrt[]{b^2-96}+-b-\text{ }\sqrt[]{b^2-96}}{2}=10 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/y9kec2i2rq23l1mbdg0eyizbytkops4zbc.png)
Simplifying, we get
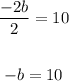
Substituting for b, we get
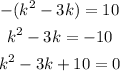
Solving for k by the Quadratic Formula method of solving quadratic equation, we get
![k=\frac{-b\pm\text{ }\sqrt[]{b^2-4ac}}{2a}](https://img.qammunity.org/2023/formulas/mathematics/college/w2j8i0cr85w6hq66wr8h191g0x3g6yy2bz.png)
Where
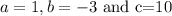
Substituting, we get
![k=\frac{-(-3)\pm\text{ }\sqrt[]{(-3)^2-(4*1*10)}}{2(1)}](https://img.qammunity.org/2023/formulas/mathematics/college/frd541rwhwns3m27e48azy9q1u7i2pe0gd.png)
![k=\frac{3\pm\text{ }\sqrt[]{9^{}-40}}{2}=\frac{3\pm\text{ }\sqrt[]{-31}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/vg469uokl0m61oght84qy1haixj1qx210i.png)
![\begin{gathered} k=\frac{3+\text{ }\sqrt[]{-31}}{2}\text{ or }k=\frac{3-\text{ }\sqrt[]{-31}}{2} \\ \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hxnbnnys9gj3culmbbrx40nbfdovjge2og.png)
Therefore, the correct answer is
![k=\frac{3+\text{ }\sqrt[]{-31}}{2}\text{ or }k=\frac{3-\text{ }\sqrt[]{-31}}{2}](https://img.qammunity.org/2023/formulas/mathematics/college/868639ws1nofodn5i0k3sd58z8av3fsxyk.png)
Alternatively,
We can use the sum of roots formula below:

So, we get
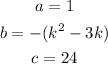
So,
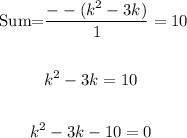
Then you can now solve from here as have done in the previous method.
Solve the quadratic equation above for k.