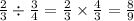Michael mows 1/3 of the yard, and the remaining is for Mel,
Note that 1 whole yard is 1
So the remaining is 1 - 1/3 = 2/3
Mel can mow 3/4 of the entire yard in 1 hour :
So in 1 whole yard, Mel can mow it for :
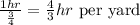
Mel's rate in mowing 1 yard is 4/3 hrs
Since Mel will mow 2/3 of the yard, multiply it by her rate will be :
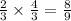
8/9 or 0.89 hour
Note that multiplication can be expressed as division,
The number of hours Mel can finish mowing the yard is :

Since the answer is same, 8/9 hour is correct.
To summarize the answers :
1. 8/9 hr or 0.89 hr
2. 2/3, as explained above.
3. The division problem is :
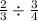
4. 8/9 hr or 0.89 hr