ANSWER
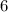
Step-by-step explanation
We want to find the first term of the sequence.
The general equation for the nth term a geometric sequence is written as:
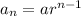
where a = first term; r = common ratio
Let us use this to write the equations for the third term and the fifth term.
For the third term, n = 3:
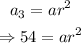
For the fifth term, n = 5:
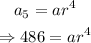
Let us make a the subject of both formula:
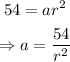
and:
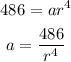
Now, equate both equations above and solve for r:
![\begin{gathered} (54)/(r^2)=(486)/(r^4) \\ \Rightarrow(r^4)/(r^2)=(486)/(54) \\ \Rightarrow r^(4-2)=9 \\ \Rightarrow r^2=9 \\ \Rightarrow r=\sqrt[]{9} \\ r=3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/osr8odjk01w67aeil6z7l4fios8ae3cedp.png)
Now that we have the common ratio, we can solve for a using the first equation for a:
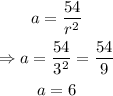
That is the first term.