Question

-11. Given points (x, y) and (x2, y2), derive the two-point form of a line. , , , 10. 13. Given that a line is parallel to the x-axis through (x, y), derive the parallel to x-axis form a line.

Answer 1

11. Given the two points (x1, y1) & (x2, y2) we will have the following line and we derivate it:

`m=(y_2-y_1)/(x_2-x_1)`
`y-y_1=m(x-x_1)\Rightarrow y=mx-mx_1+y_1`

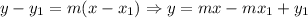
It's derivative is:

`(\delta y)/(\delta x)=m=(y_2-y_1)/(x_2-x_1)`

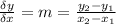
This is since the derivative of constants is 0 and the only variable accompanied m. This is proof that the derivative of a function can be interpreted as the slope of the function at that point.

13. If we have that the line is parallel to the x-axis and passes through the point (x1, y1), we will have that the line is a constant function, so when we derivate no matter the point, it will be equal to 0.

That is:

`y=x_1`
`(\delta y)/(\delta x)=0`

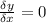
***Explanation:

point 11:

Since we are given two points (x1, y1) & (x2, y2), we will always have that the slope of the line that passes through those points will always have the form: