Question

Find the slope and y intercept of the line shown below question number 4

Answer 1

The image of the line provided seems to go through the following points:

(0, 4) , (-4, 5), and (4, 3)

Knowing at least two points is essential to calculate the slope via the formula:

`\text{slope}=(y_2-y_1)/(x_2-x_1)`

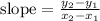
so, for example if we use the points (0, 4) and (-4, 5) to calculate the slope, we get:

`\text{slope}=(5-4)/(-4-0)=-(1)/(4)`

Therefore, the slope is -1/4 (negative one fourth)

Notice as well that one of the points we chose is (0, 4) which in fact is the y-intercept of the line (the point at which the line crosses the y-axis ).

so we have al the elements to built the equation of this line:

slope = -1/4

y intercept = 4 for the (0, 4) on the plane

Then the equation could be built using:

y = (-1/4) x + 4