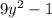It is important to know that a Product is the result of a multiplication.
You have the following expression given in the exercise:
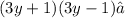
Notice that it is the multiplication of two Binomials and it has this form:
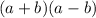
By definition:
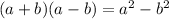
This is called "Difference of two squares".
You can identify that, in this case:
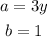
Therefore, you get:
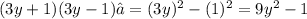
The answer is: