Question

The midpoint of a segment can be found using the formulas for a directed line segment, x =C DaQ+bX2-X1) + X, and46]«y =aa + b-6/2 – Yı) + y1. When using these formulas to find a midpoint, which is true?O a = 1 and b= 2a = 2 and b = 1a = 1 and a + b = 2a = 2 and a + b = 2NextSubmitSave and ExitMark this and return

Answer 1

In general, the formula to find the midpoint of a line segment which ends have the coordinates (x₁,y₁) and (x₂,y₂) is given by

`M=((x_2+x_1)/(2),(y_2+y_1)/(2))`

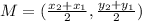
Working with the formula we are given, for the x coordinate of the midpoint we have:

`x=((a)/(a+b))(x_2-x_1)+x_1=(a(x_2-x_1))/(a+b)+((a+b)x_1)/(a+b)`

In order for this to be like the previous formula, we have the following equation:

`(a(x_2-x_1))/(a+b)+((a+b)x_1)/(a+b)=(x_2+x_1)/(2)`

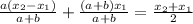
From here, we see that a+b must be equal to 2, so:

`(a(x_2-x_1))/(2)+\frac{2x_1_{}}{2}=(ax_2-ax_1)/(2)+(2x_1)/(2)=(ax_2-ax_1+2x_1)/(2)=(x_2+x_1)/(2)`

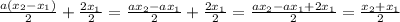
In order for this last equation to be true, a must equal 1:

`(x_2-x_1+2x_1)/(2)=(x_2+x_1)/(2)`

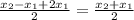
Let's verify this with the formula for the y coordinate of the midpoint:

`((1)/(2))(y_2-y_1)+y_1=(y_2-y_1)/(2)+y_1=(y_2-y_1)/(2)+(2y_1)/(2)=(y_2-y_1+2y_1)/(2)=(y_2+y_1)/(2)`

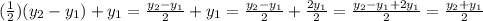
Since using our previous deduction leads us to the correct formula for the y coordinate of the midpoint as well, we can conclude that a=1 and a+b=2.