Step-by-step explanation
We are told that the tangent of an angle x is equal to 0.9004. In order to solve this equation for x we can use the arctangent function that has this property:
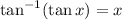
Then we can apply the arctangent to both sides of our equation:
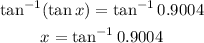
So our angle is the arctangent of 0.9004 which can be found using a calculator. However calculators oftenly work with radians and we need to express x in degrees. In order to transform the result from radians to degrees we have to perform the following operation:

Answer
Wheter we round to the nearesth tenth, hundreth or thousanth the answer is 42°.