Given the slope of the line:

And this point on the line:
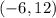
(a) By definition, the Slope-Intercept Form of the equation of a line is:

Where "m" is the slope and "b" is the y-intercept.
In this case, you can substitute the slope and the coordinates of the known point into that equation, and then solve for "b", in order to find the y-intercept:
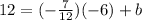
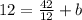
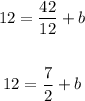
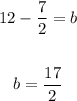
Therefore, the equation of this line in Slope-Intercept Form is:
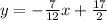
(b) The Standard Form of the equation of a line is:
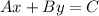
Where A, B, and C are integers, and A is positive.
In this case, you need to add this term to both sides of the equation found in Part (a), in order to rewrite it in Standard Form:
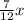
Then, you get:

Hence, the answers are:
(a) Slope-Intercept Form:
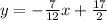
(b) Standard Form:
