Given the system of equations:
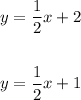
Let's solve the system using graphing method.
Let's plot both equations on a graph. The point where both lines meet.
• Equation 1:
Let's plot using 3 points.
Substitute random values of x and solve for y.
We have:
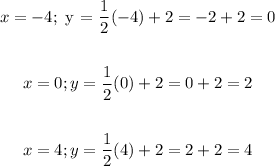
For equation 1, we have the points:
(x, y) ==> (-4, 0), (0, 2), (4, 4)
Plot the points and connect the points with a straight line.
• Equation 2:
Let's create 3 points:
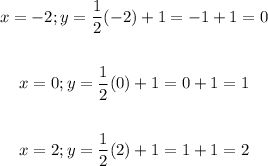
FOr equation 2, we have the points:
(x, y) ==> (-2, 0), (0, 1), (2, 2)
Now, plot the points and connect using a straight line.
We have the graph of both equations below:
From the graph, we can see that both lines do not meet at any point.
They are parallel lines,
Since they will not meet at any point, there is NO SOLUTION.
ANSWER:
No solution.