First, we need to find the length of the bottom base.
The next right triangle is formed inside the trapezoid:
From definition:
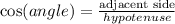
Substituting with data from the picture:
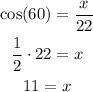
Since there are two congruent angles, then the opposite sides are also congruent, that is, there are two sides with lengths equal to 22.
Then, the length of the bottom base is 11 + 25 + 11 = 47.
The perimeter of the figure is obtained by adding the length of all its sides. In this case, the perimeter is 47 + 22 + 25 + 22 = 116
The area of a trapezoid is computed as follows:
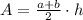
Where a and b are the bases and h is the height
The height of the shape can be calculated with the help of the previous right triangle, as follows:
![\begin{gathered} \sin (angle)=\frac{\text{opposite side}}{hypotenuse} \\ \sin (60)=(h)/(22) \\ \frac{\sqrt[]{3}}{2}\cdot22=h \\ 11\cdot\sqrt[]{3}=h \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/g1wlaackeitmhcez49cc6uxeccrwjp9lrs.png)
Substituting into area's formula:
![\begin{gathered} A=(25+47)/(2)\cdot11\cdot\sqrt[]{3} \\ A=36\cdot11\cdot\sqrt[]{3} \\ A=396\cdot\sqrt[]{3}\approx686 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/5nb2jx3t9vpy9z7qv72ki80ffhjxllderd.png)