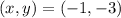Answer:
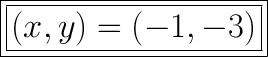
Explanation:
multiply first equation by 4 and second by 3 respectively:

combine the equations:
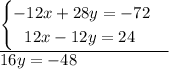
divide both sides by -48:
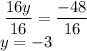
substitute the value of y to the second equation

simplify multiplication:

cancel 12 from both sides:

divide both sides by 4
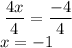
therefore our solution is