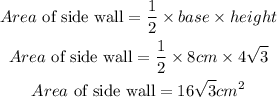Answer:
a) 64cm
b) 64 square cm
c) 4√3 cm
d) 16√3 square cm
Explanations:
A regular quadrilateral pyramid with equilateral triangles is as shown below;
1) The pyramid has 8 side lengths, hence the sum of the length of all the sides is given as:
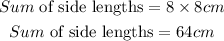
2) Since the triangular sides are equilateral, the base of the pyramid will be a square with side length of 8cm. The area of the base is expressed as:
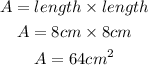
3) Since one side wall is an equilateral triangle, the height will be perpendicular to the base as shown:
In order to determine the height, we will use the Pythagorean theorem as shown:
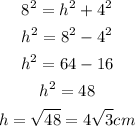
4) The area of the side wall is equivalent to the area of the triangle expressed as: