The absolute value function is given below as
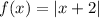
Concept: We will have to explain what is meant by an odd function, even function, or neither
Even function: A function is said to be even if it has the equality below
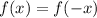
is true for all x from the domain of definition.
An even function will provide an identical image for opposite values.
Odd function:A function is odd if it has the equality below
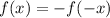
is true for all x from the domain of definition.
An odd function will provide an opposite image for opposite values.
Neither: A function is neither odd nor even if neither of the above two qualities is true, that is to say:
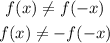
Given that
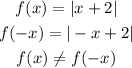
Also,
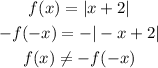
Therefore,
We can conclude that f(x) = |x+2| is NEITHER an even nor a odd function