Question

Part A Estimate 10/12 - 3/8 using benchmark values. Your equation must show the estimate for each fraction and the final estimate for the expression.Part BSolve 10/12 - 3/8Part Ccalculate the difference between your stimate in Part A and the actual value calculated in Part B.Show the solution as an equation Based on the results was your estimate in Part A reasonable?

Answer 1

`\begin{gathered} A\text{. 1/2} \\ B\text{. 11/24} \\ C\text{. }(1)/(24) \\ \end{gathered}`

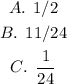
Yes, the calculations in A were reasonable because the difference is pretty close to 0.

Explanation:

For part A,

-estimate the fraction 10/12 using 1/2 as our benchmark

The lower range is 1/2 and the upper range is 1

The halfway point is:

`\begin{gathered} (1)/(2)\cdot((1+2))/(2) \\ (1)/(2)\cdot(3)/(2)=(3)/(4) \end{gathered}`

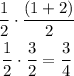
Therefore, our range is 1/2 < 3/4 < 1

10/12 ≥ 3/4, we round up to 1

-estimate the fraction 3/8 using the 1/2 as our benchmark:

The lower range is 0 and the upper range is 1/2

The halfway point is:

`(1)/(2)\cdot(1)/(2)=(1)/(4)`

Therefore, our range is 0 < 1/4 < 1/2

3/8 ≥ 1/4, we round up to 1/2

`(2)/(2)-(1)/(2)=(1)/(2)`

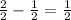
For part B, the denominators are 12 and 8, so the LCM would be;

`\text{LCM}=24`

Then, we make a common denominator and subtract the numerators

`\begin{gathered} (10)/(12)-(3)/(8)=(20)/(24)-(9)/(24) \\ (10)/(12)-(3)/(8)=(11)/(24) \end{gathered}`

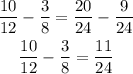
For part C, compute the difference between the two results from parts A and B:

`(1)/(2)-(11)/(24)=(1)/(24)`

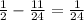
Yes, the calculations in A were reasonable because the difference is pretty close to 0.