Here, the dividend is x^3-6x^2+11x+6 and the divisor is x-2.
Put the value of divisor as 0 implies,
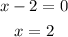
Find f(2) implies,
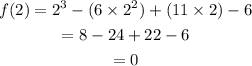
Therefore, x-2 is a factor of the polynomial.
Pu the value 0 for x+4 gives,
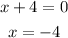
Find f(-4) gives,
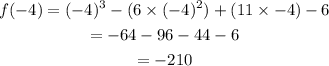
Therefore, x+4 is not a factor of polynomial.
Hence, Option C.