Question

How many years will it take for an initial investment of $10,000 to grow to $25,000? Assume a rate of interest of 3% compounded daily.

Answer 1

The formula for compounded interest is the following:

`A=P(1+(r)/(n))^(nt)`

Where A is the final amount, P is the principal, the initial investment, r is the annual rate of interest, n is how many times it is compounded per year and t is the time in years.

So, assuming the given rate of interest is annual, we have:

`\begin{gathered} A=25000 \\ P=10000 \\ r=3\%=0.03 \\ n=365 \\ t=? \end{gathered}`

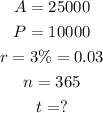
Where we got n = 365 because it is compounded daily and there are 365 days in an year.

So let's start by solving for t:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ (A)/(P)=(1+(r)/(n))^(nt) \\ \log (A)/(P)=\log (1+(r)/(n))^(nt) \\ \log (A)/(P)=nt\log (1+(r)/(n)) \\ (\log(A)/(P))/(n\log(1+(r)/(n)))=t \\ t=(\log(A)/(P))/(n\log(1+(r)/(n))) \end{gathered}`

Where the log base can be anyone, but it has to be the sme for both log.

Let's calculate the numerator and denominator separately first, using base 10:

`\log _{}(A)/(P)=\log (25000)/(10000)=_{}\log 2.5=0.39794\ldots`
`\begin{gathered} n\log (1+(r)/(n))=365\log (1+(0.03)/(365))=365\log (1+0.0000821918\ldots)= \\ =365\log (1.0000821918\ldots)=365\cdot0.000035694\ldots=0.013028\ldots \end{gathered}`

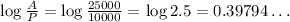
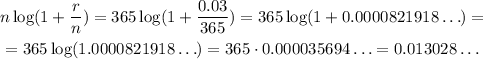
Putting them together, we have:

`t=(\log(A)/(P))/(n\log(1+(r)/(n)))=(0.39794\ldots)/(0.013028\ldots.)=30.54\ldots\approx31`

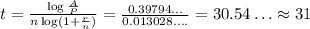
So, it will take between 30 and 31 years, closer to 31 years for it to grow to $25,000.