To find the point S we first need to find the equation of the circle which is given by:

where (h,k) is the center and r is the radius.
In this case we don't have the radius but we know that the radius is the distance between the center and any point on the circle, then the radius is equal to the distance:
![\begin{gathered} r=d(A,R)=\sqrt[]{(5-3)^2+(4-(-1))^2} \\ =\sqrt[]{4+25} \\ =\sqrt[]{29} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ug5zz3axbtouz0lj1mb1cqguh7o42rwylp.png)
hence the equation of the circle is:
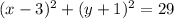
Now that we have this equation we need to determine which of the options given fullfil the equation. From the options given we conclude that the only point that fullfils the equation is the point D, this come from the fact that:
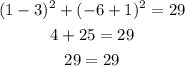
Therefore this point is in the circle. Therefore we conclude that the coordinates of point D are (1,-6) and the answer is D.
This can be seen in the graph below: