Question

Just need help and a simple way to solve this

Answer 1

4.5 is the answer to the question

Answer 2

The length of the third leg is

Explanation:

The figure given is a right-angled triangle.

To find the third length of the triangle, we need to apply Pythagora's theorem

It states that

`\begin{gathered} (Hypotenuse)^2=(opposite)^2+(adjacent)^2 \\ \end{gathered}`

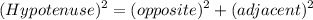
The third length of the triangle is the hypotenuse because it is the longest

`\begin{gathered} (Hypotenuse)^2=4^2+2^2 \\ (Hypotenuse)^2\text{ = 16 + 4} \\ (Hypotenuse)^2\text{ = 20} \\ \text{ Take the squareroots of both sides} \\ \text{ }\sqrt[]{(Hypotenuse)^2\text{ }}\text{ = }\sqrt[]{20} \\ \text{Hypotenuse = }4.472 \\ \text{Hypotenuse }\approx\text{ 4.5} \end{gathered}`

Hence, the length of the third leg is 4.5