Answer:
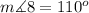
Step-by-step explanation:
The angles 4 and 8 are equal; therefore,
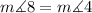
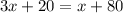
Subtracting x from both sides gives
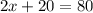
Subtracting 20 from both sides gives
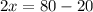
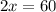
Finally, dividing both sides by 2 gives
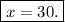
With the value of x in hand, we now find the measure of angle 8.
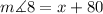
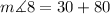
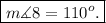
Hence, the measure of angle 8 is 110.