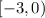Question

Y=-x^2-2x+3 what is the vertex of the graph? Answer an order pair.

Answer 1

Given:

`y=-x^2-2x+3`

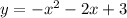
a) To find the vertex:

Here, a=-1, b=-2, and c=3

We know that the formula to find the x- coordinate of the vertex is given by,

`\begin{gathered} -(b)/(2a)=-((-2))/(2(-1)) \\ =-1 \end{gathered}`

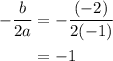
Substitute x=-1 in the given equation we get,

`\begin{gathered} y=-(-1)^2-2(-1)+3 \\ =-1+2+3 \\ =4 \end{gathered}`

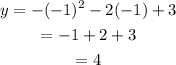
Hence, the vertex of the graph is (-1, 4).

b) To find the range of the graph:

Let us find the y-intercept.

Put x=0, we get

`\begin{gathered} y=-(0)^2-2(0)+3 \\ =3 \end{gathered}`

From the figure, we observe that

The range of the graph is

`\lbrack0,4\rbrack`

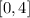
c) To find the domain of the graph:

Let us find the x-intercept.

Put y=0, we get

`\begin{gathered} -x^2-2x+3=0 \\ (x+3)(x-1)=0 \\ x=-3,1 \end{gathered}`

From the figure, we observe that,

The domain of the graph is,

`\lbrack-3,0)`