Lets draw a picture of our quadrilateral:
In order to find the area, we can divide our parallelogram in 2 triangles:
The area of triangle AHT is given by
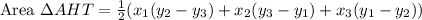
where
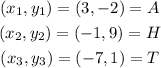
By substituting these points into the given formula, we get

which gives
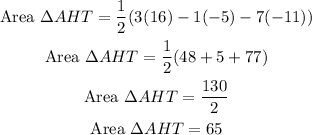
Similarly, for the area of triangle AHM, we can choose
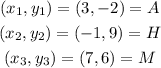
By substuting in our area formula, we get
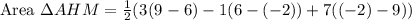
which gives

Then, the total area is given by
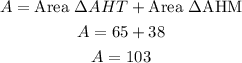
then, the answer is 103 units squared.