Question

Find the values for A and B. explain of show your reasoning

Answer 1

The value of a is 5, and b is 6.

Step-by-step explanation:

The points on the line are (6,10), (a,8), (4,b) and (2,2).

• The slope of a straight line is always constant.

First, determine the slope using the points (6,10) and (2,2).

`\begin{gathered} \text{Slope}=\frac{Change\text{ in y-axis}}{Change\text{ in x-axis}} \\ =(10-2)/(6-2) \\ =(8)/(4) \\ =2 \end{gathered}`

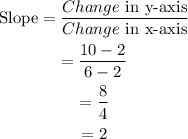
Next, using points (6,10) and (a,8):

`\begin{gathered} m=(10-8)/(6-a) \\ 2=(2)/(6-a) \\ \text{Cross multiply} \\ 2(6-a)=2 \\ 12-2a=2 \\ -2a=2-12 \\ -2a=-10 \\ a=-(10)/(-2) \\ a=5 \end{gathered}`

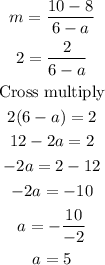
Next. using points (6,10) and (4,b):

`\begin{gathered} m=(10-b)/(6-4) \\ 2=(10-b)/(2) \\ \text{Cross multiply} \\ 10-b=2*2 \\ 10-b=4 \\ b=10-4 \\ b=6 \end{gathered}`

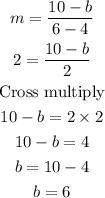
The value of a is 5 and b is 6.