Question

Suppose each cube in this right rectangular prism is a 1/2-in unit cube

Answer 1

The length of each cube is given below as

`l=(1)/(2)in`

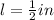
Concept:

To figure out the dimension of the prism, we will calculate the number of cubes to make the length,width and height and multiply by 1/2

To figure out the length of the prism,

we will multiply 1/2in by 5

`\begin{gathered} l=(1)/(2)in*5 \\ l=2.5in \end{gathered}`

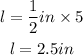
To figure out the width of the prism,

we will multiply 1/2in by 4

`\begin{gathered} w=(1)/(2)in*4 \\ w=2in \end{gathered}`

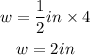
To figure out the height of the prism,

we will multiply 1/2 in by 3

`\begin{gathered} h=(1)/(2)in*3 \\ h=(3)/(2)in=1.5in \end{gathered}`

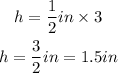
Hence,

The dimensions of the prism are

Length = 2.5in

Width = 2in

Height = 1.5 in

2.5in by 2in by 1.5in

Part B:

To figure out the volume of the prism, we will use the formula below

`\begin{gathered} V_(prism)=base\text{ area}* height \\ V_(prism)=l* w* h \\ l=2.5in,w=2in,h=1.5in \end{gathered}`

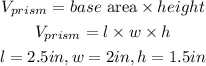
By substituting the values, we will have

`\begin{gathered} V_(pr\imaginaryI sm)=l* w* h \\ V_{pr\mathrm{i}sm}=2.5in*2in*1.5in \\ V_{pr\mathrm{i}sm}=7.5in^3 \end{gathered}`

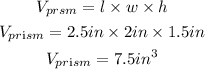
Alternatively, we will calculate below by calculate the volume of each cube and then multiply by the total number of cubes

`\begin{gathered} volume\text{ of each cube=} \\ =l^3=((1)/(2))^3=(1)/(8)in^3 \\ The\text{ total number of cubes =} \\ =5*4*3 \\ =60cubes \\ Volume\text{ of the prism } \\ =(1)/(8)in^3*60 \\ =7.5in^3 \end{gathered}`

Hence,

The volume of the prism is = 7.5in³