Question

I need help checking to make sure my work is correct. Start with the basic function f(x) = 2x. If you have an initial value of 1, then you end up with the following iterations:f(1) = 2 x 1 = 2f^2 (1) = 2 x 2 x 1 = 4f^3 (1) = 2 x 2 x 2 x 1 = 8The question Part 1: If you continue the pattern, what do you expect would happen to the numbers as the number of iterations grows? Check your result by conducting at least 10 iterations. I put: f^4 (1) = 2 x 2 x 2 x 2 x 1 = 16f^5 (1) = 2 x 2 x 2 x 2 x 2 x 1 = 32f^6 (1) = 2 x 2 x 2 x 2 x 2 x 2 x 1 = 64f^7 (1) = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 1 = 128f^8 (1) = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 1 = 256f^9 (1) = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 1 = 512f^10 (1) = 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 2 x 1 = 1024Part 2: Repeat the process with an initial value of -1. What happens as the number of iterations grows?

Answer 1

Given: The function below:

`f(x)=2x`

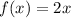
To Determine: The interation with initial value of 1

When the initial value is 1, it means that x = 1

If x =1, we can determine f(1) by the substituting for x in the function as shown below:

`\begin{gathered} f(x)=2x \\ x=1 \\ f(1)=2(1)=2*1=2 \end{gathered}`
`f^2(1)=2^2*1=2*2*1=4`

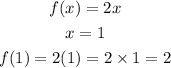
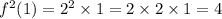
Part 1:

It can be observed that as the number of iterations grow, the number increase in powers of 2

This can be modelled as

`f^n=2^n*1=2^n`
`f^(10)=2^(10)*1=1024`

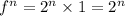
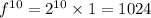
Part 2:

If we repeat the process with an initial value of -1. As the number of iterations grows, the number can be modelled as

`\begin{gathered} f^(-n)=2^(-n)*1 \\ f^(-1)=2^(-1)*1=(1)/(2)*1=(1)/(2) \\ \text{For initial value of -2, we would have} \\ f^(-2)=2^(-2)*1=(1)/(2^2)*1=(1)/(4) \end{gathered}`

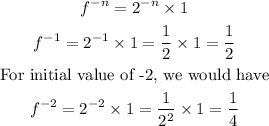
So, as the initial value decreases, it can be observed by the above calculations that the number would be decreasing by the the reciprocal of the power of 2.