Question

Since f is parallel to line g, use the diagram to the right right to answer the following question (I need help with problem D and the graph right next to it )

Answer 1

Given,

The line f and g are parallel lines.

a)The measure of angle 2 is 117 degree.

By exterior atlernate angle property,

`\begin{gathered} \angle2=\angle7 \\ \angle7=117^(\circ) \end{gathered}`

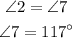
The measure of angle 7 is 117 degree.

b)The measure of angle 4 is 68 degree.

By sum of adjacent angle between two parallel lines property,

`\begin{gathered} \angle4+\angle6=180^(\circ) \\ \angle6=180^(\circ)-68^(\circ) \\ \angle6=112^(\circ) \end{gathered}`

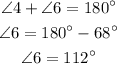
The measure of angle 6 is 112 degree.

c)The measure of angle 5 is 32 degree.

By alternate interior angle property,

`\begin{gathered} \angle4=\angle5^{} \\ \angle4=32^(\circ) \end{gathered}`

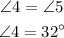
The measure of angle 4 is 32 degree.

d)The measure of angle 7 is 121 degree.

By corresponding angle property,

`\begin{gathered} \angle7=\angle3^{} \\ \angle3=121^(\circ) \end{gathered}`

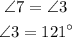
The measure of angle 3 is 121 degree.