We define the following notation:
• z = cost of an item from shelf A,
,
• y = cost of an item from shelf B.
From the statement, we know that:
• 3 items from shelf A and 2 from shelf B cost $26, so we have:
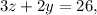
• 2 items from shelf A and 5 from shelf B for $32, so we have:
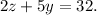
We have the following system of equations:
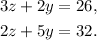
1) To solve this system, we multiply the first equation by 2 and the second equation by 3:
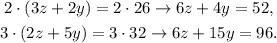
2) We subtract equation 1 to equation 2, and then we solve for y:

We found that y = 4.
3) We replace the value y = 4 in the first equation, and then we solve for z:
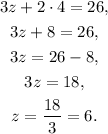
Answer
The cost of the items are:
• z = 6, for items from shelf A,
,
• y = 4, for items from shelf B.