Question

4 N2H3CH3 (l) + 5 N2O4 (l) →12 H2O(g) + 9 N2(g) + 4 CO2 (g)The enthalpy of formation for liquid methylhydrazine is +53 kJ/mol and the enthalpy of formation for liquid dinitrogen tetroxide is -20 kJ/mol. Calculate ∆H° for this reaction, ignore significant digits for this question.

Answer 1

Step-by-step explanation

The given chemical equation for the reaction is:

`4N_2H_3CH_3(l)+5N_2O_4(l)\text{ }→\text{ }12H_2O\left(g\right)+9N_2\left(g\right)+4CO_2(g)`

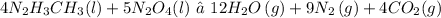
From the given table and question, the enthalpies of formation of the reactants ad products are:

`\begin{gathered} ∆H_f°(N_2H_3CH_(3(l)))=+53\text{ }kJ\text{/}mol \\ \\ ∆H_f°(N_2O_(4(l)))=-20\text{ }kJ\text{/}mol \\ \\ ∆H_f°(H_2O_((g)))=-258.8\text{ }kJ\text{/}mol \\ \\ ∆H_f°(N_(2(g)))=0\text{ }kJ\text{/}mol \\ \\ ∆H_f°(CO_(2(g)))=-393.5\text{ }kJ\text{/}mol \end{gathered}`

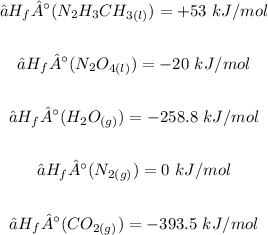
The ∆H° for this reaction can be calculated using the formula below:

`\Delta H_(rxn)\degree=ΔH_f^(\degree)(products)-ΔH_f^(\degree)(reactants)`

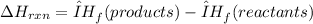
Put the each enthalpy of formation of the reactants and the products into the formula:

`\begin{gathered} \Delta H_(rxn)\degree=[12(-258.8)+9(0)+4(-393.5)]-[4(+53)+5(-20)] \\ \\ \Delta H_(rxn)\degree=[-3105.6+0-1574]-[212-100] \\ \\ \Delta H_(rxn)\degree=-4679.6-112 \\ \\ \Delta H_(rxn)\degree=-4791.6\text{ }kJ\text{/}mol \end{gathered}`

Therefore, the ∆H° for this reaction is -4791.6 kJ/mol.