Question

Rita is a software saleswoman. Let y represent her total pay (in dollars). Let x represent the number of copies of English is Fun she sells. Suppose that x and y are related by the equation 1900+110x=Y.

Answer 1

, if she does not sell any of English,x = The number of copies of English is Fun she sells

y = Total pay

`y=1900+110x`

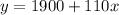
Therefore,

a.

Her change in total pay for each copy of English is fun can be computed below.

(0, 1900) (1, 2010)

`m=(2010-1900)/(1-0)=110`

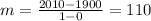
Her change in total pay for each copy of English is fun she sells = $110

b.

Her total pay if she does not sell any of English is fun is the y-intercept. Therefore,

`\begin{gathered} y=1900+110x \\ y=1900+110(0) \\ y=\text{ \$1900} \end{gathered}`

Her total pay if she does not sell any of English is fun = $1900

Note you can model it to the slope-intercept equation.

`\begin{gathered} y=mx+b \\ \text{where} \\ m=\text{change in total pay for each copy of English is fun she sells } \\ b=\text{Her total pay if she does not sell any of English is fun} \end{gathered}`