To answer this question, we need to find the area of the square, and then the area of the circle. Then, we need to subtract from the area of the circle, the area of the square.
The area of the square is given by the formula:
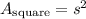
The side of the square is 7cm. Then, the area is:
![A_{\text{square}}=(7\operatorname{cm})^2\Rightarrow A_(square)=49\operatorname{cm}^2]()
Now, the area of the circle is given by the formula:
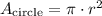
The diameter of the circle is equal to 10cm. The radius of the circle is half of the measure of the diameter. Then, the radius is equal to 10/2 ---> r = 5cm. Then, we have:
![A_{\text{circle}}=\pi\cdot(5\operatorname{cm})^2\Rightarrow A_(circle)=\pi\cdot25\operatorname{cm}\approx78.54\operatorname{cm}^2]()
Now, to find the shaded area, we need to subtract from this area, the area of the square:
![A_{\text{shaded}}=A_{\text{circle}}-A_{\text{square}}=78.54\operatorname{cm}-49\operatorname{cm}=29.54\operatorname{cm}^2]()
Therefore, the shaded area is closest to 29.5 square centimeters (third option) (if we round our result to the nearest tenth.)