Question

Х о 1 2 3 4 у -5 4 13 22 31

Answer 1

We can take any 2 points both from x and y and use the equation of a line formula to find out the equation of the line represented by the points in the table.

Let's take the points:

`\begin{gathered} (x_1,y_1)=(0,-5) \\ (x_2,y_2)=(1,4) \end{gathered}`

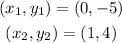
The equation of a line formula is:

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

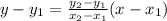
Let us plug in the points into this formula and do a little algebra to re-arrange the equation in the slope-intercept form, which is y = mx + b. The steps are shown below:

`\begin{gathered} y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1) \\ y-(-5)=(4-(-5))/(1-0)(x-0) \\ y+5=(4+5)/(1)(x) \\ y+5=(9)/(1)(x) \\ y+5=9x \\ y=9x-5 \end{gathered}`

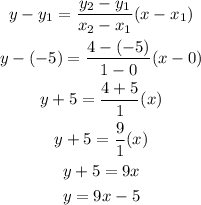
The slope-intercept form is given by:

`y=9x-5`

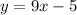
Where 9 is the slope and -5 is the y-intercept (y-axis cutting point)