Given
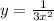
2x+3y=18
Find
Prove algebraically how many intwrsections there will be between the railroad
Step-by-step explanation
The graph of 2x+3y=18 is as the picture
2x+3y=18
when x=0, 0+3y=18 => y=6 =>(0,6)
when y=0, 2x+0=18 => x=9 => (9,0)
The intersection between the railroad and the highway is 0 because the graph of the railroad and the graph of the highway are parallel, that means they have no intersection
(b)
Assume the railroad can be found using the equation y=3/2x+b
when x=0 => y=8
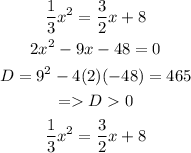
has two roots, and there are 2 intersections
Final Answer
(a) No intersection
(b) Two intersections